Guide 11-4. Angular Momentum

This guide restates some of the information in text sections 11-6,7 and introduces some additional information.

Definitions

Just as torque is the analogue of force for rotational motion of rigid objects, angular momentum is the analogue of linear momentum. For a rigid object with moment of inertia I rotating about an axis with angular velocity ω, the angular momentum is defined as L = Iω. A special case is that of a point particle of mass m rotating in a circle of radius r at speed v. The moment of inertia of such a particle is mr²,and the angular speed is ω = v/r, hence, L = mr²(v/r) = rmv. Note the similarity of this expression to that for the linear momentum of a particle, namely, p = mv. One multiplies by r to obtain the angular momentum. We emphasize, though, that this latter result applies to the special case of a particle in uniform circular motion.

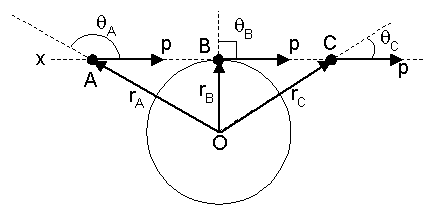
Particles in straight line motion may also have angular momentum if the particle is moving off-axis. See Figure 1 below. A particle of mass m moves at velocity v along straight line x. Three successive positions of the particle are shown. Relative to an axis at point O, the successive position vectors of the particle are r_A, r_B, and r_C.The angular momentum of the particle is the product of the linear momentum, p, and the component rsinθ of the position vector. Note that the angle between the position and velocity vectors is defined in the same way as that for torque. Extend the position vector as shown by the dotted lines in Figure 1. The angle between the extension of r and the momentum is the angle θ. For the three positions shown, the angular momenta are therefore L_A = pr_Asinθ_A, L_B = pr_Bsinθ_B, and L_C = pr_Csinθ_C. Note that all three products of rsinθ are equal to the same thing, namely, the perpendicular distance from point O to line L. Thus, we can write for a point particle with linear momentum p that the angular momentum is equal to the product of p and the perpendicular distance from the axis of rotation to the line of p: .

Figure 1	Figure 2

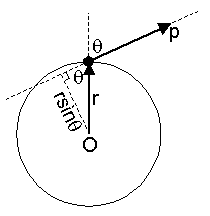In the example of Figure 1, the particle is moving tangent to the circle centered on the axis at O. However, this is not required. Suppose the particle is moving at some other angle such as that shown in Figure 2. The same formula, , is used for the calculation of angular momentum. See Figure 2 for how the distance rsinθ is found.

Conservation Laws

In the example described in Figure 1 above, the particle had a constant linear momentum. The net, external force acting on the particle was 0; hence, linear momentum was conserved. Note that angular momentum was also conserved, sincedid not change. For angular mometum, the condition for conservation is that the net, external torque on the system is 0. We state both conservation laws below in their general forms.

Linear Momentum	Angular Momentum
Fnet,ext Δt = Δpnet	τnet,ext Δt = ΔLnet

Figure 3

Recall that Δp_net represents the total change of linear momentum of all the objects in the system. Likewise, ΔL_net represents the total change of angular momentum of all the objects in the system.

If the system is chosen so that F_net,ext = 0, we can write: P_i = P_f, where P represents the total momentum of the objects in the system at a particular time. Likewise, if the system is chosen so that τ_net,ext = 0, then we can write L_i = L_f, where L is taken to represent the total angular momentum of the objects in the system at a particular time.

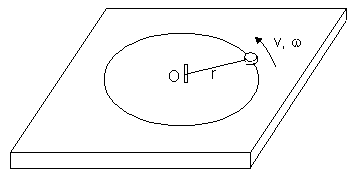
Let's see how the conservation laws are applied to a very simple situation of a puck moving in a horizontal circle at constant speed at the end of a string of negligible mass. Suppose that the string is attached to a post on an air table, and the puck is set into circular motion. See Figure 3 to the right. Taking the system to be just the puck, the external forces on the system are the normal force of the table, the weight of the puck, and the tension of the string. We assume friction to be negligible on the air table. Since the normal and weight forces balance on the horizontal surface, we are left with F_net,ext = T. Therefore, linear momentum is not conserved in this situation. We can also see this is true from the fact that the direction of the puck's velocity, hence momentum, is changing continuously.

Let's look at the torques for the same situation. Again, we'll take the puck to be the system. The axis of rotation will be the physical axis, O, at the post. The normal and weight forces both exert torques with moment arms equal to the radius, r, of the path; however, these torques are opposite and add to 0. The tension force exerts no torque, because its line of action passes through the axis. Therefore, the net, external torque on the puck is 0, and angular momentum is conserved. We can also see this from the fact that the quantity for the puck doesn't change. The distance is always equal to r, and the magnitude of the linear momentum, p, is constant.

You may have noticed that we treated L in the above example as a magnitude, saying that the magnitude of L doesn't change, whereas we treated the linear momentum as a vector, saying the the direction of the vector was changing; hence, the linear momentum wasn't conserved. It's important to realize, though, that angular momentum is also a vector, and the relationship given above, τ_net,ext Δt = ΔL_net, is a vector relationship. Therefore, we need to say something about the vector nature of angular momentum and why it doesn't change in the example of the ball on a string.

Figure 4	Figure 5

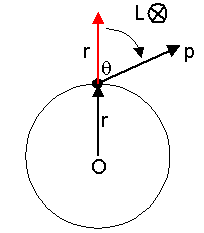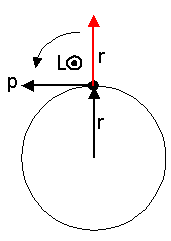
Let's apply this method to the ball and the string. See Figure 4. We've translated the r vector upward (the red vector) so that its tail coincides with that of p. When you hold your right hand so that your fingers naturally curl from r to p, your thumb points toward you, out of the screen. That's the direction of L. In order to represent this direction in a plane, we use a circle with a dot in the middle. This indicates a vector pointing out of the screen. Think of it as looking at the head of an arrow coming toward you. You can see that L will also be perpendicular to the plane of r and p; hence, the direction of L doesn't change as the puck rotates. Therefore, both the magnitude and direction of L are unchanged, and L is conserved.

Let's look at another example of determining the direction of the angular momentum. Consider the situation of Figure 2. We've redrawn it in Figure 5, translating the r vector to the tail of p. In order to curl your fingers from r to p, you have to orient your hand so that your thumb points into the screen. This direction is indicated on the plane as a circle with an X in it. Think of this as looking at the feathers of an arrow going away from you.

As you can see from the above example of the ball on a string, angular momentum can be conserved while linear momentum isn't. The reverse is also possible, linear momentum can be conserved while angular momentum isn't. You'll do an exercise later in which the latter is the case.

Examples of Conservation of Angular Momentum

The textbook provides several examples in section 11-7. Example 11-9 has to do with changing your rate of rotation on a spinning stool just by redistributing your mass. V114 deals with this situation.

Other examples in the textbook reading involve rotational collisions. Study these before doing WebAssign E.11.3.

© North Carolina School of Science and Mathematics, All Rights Reserved. These materials may not be reproduced without permission of NCSSM.